.
Po wielu różnych koncepcjach zachowania się pnia po kolizji z brzozą zależnych od tego, czy ma on zrobić miejsce dla skrzydła poruszającego się z pozytywnym kątem natarcia lub bez, Binienda w końcu chyba "ustabilizował" właściwości mat.143 czyli pnia, skoro przeszedł do takich szczegółów, jak animowanie zachowania slotu i poniższy zrzut obrazuje dokładnie zachowanie pnia po przecięciu go przez skrzydło.
Rys.2
Poza tym na Figure 82 w
https://www.fhwa.dot.gov/publications/research/safety/04096/04096.pdf
znajdujemy wyraźnie paraboliczne początkowe fragmenty potwierdzajace, że w tym zakresie energia potencjalna jest proporcjona do kwadratu wychylenia, z tego zaś, że jej pochodna po wychyleniu, czyli siła, jest proporcjonalna do samego wychylenia. Tak więc możemy zupełnie spokojnie stosować wzór na strzałkę ugięcia
delta = F * l^3 * 4 / 3 * E * Pi * r^4
z którego wyliczazmy siłę
F(delta) = delta * 3 * E * Pi * r^4 / L^3 * 4
gdzie r - promień ; L - długość, czyli wysokość pnia ; delta - strzałka ugięcia ; E - moduł Younga sprężystości. (we wzorze kursywą wyróżniłem czynniki zwykle wyodrębniane jako moment bezwładności przekroju).
Praca wykonana na pokonanie siły spężystości to:
∫F(delta)*d(delta) w granicach od 0 do maksymalnej strzałki ugięcia.
Dla dolnej części pnia ta praca, czyli energia potencjalna sprężystości wynosi 195KNm a dla górnej 55KNm , co w sumie daje 250KNm.
Taką energię, tym razem kinetyczną, masa pnia musiała uzyskać w czasie kontaktu ze skrzydłem. Jeżeli ten kontakt odbywalby się na drodze równej długosci cięciwy skrzydła, to mamy sytuację z symulacji "bielskiej" - uszkdzone dolne poszycie, jeżeli natomiast na drodze równej średnicy pnia, to prowadzi do średniej siły
568KN -
około dwukrotnie przekraczjącej szacunki siły potrzebnej do zniszczenia okolicy pierwszego dźwigara, w tym moje wykonane na podstawie eksperymentu strzelania garnkiem (
http://mjaworski50.blogspot.com/2014/07/wybuchy.html ). Sytuacja trochę przypomina zapętlenie się Biniendy z grubościami poszycia i dźwigara, kiedy to we wszystkich symulacjach przednia krawędź rozpadała się jak papier - nawet kiedy miała 5mm grubości, a pierwszy dźwigar bez szwanku dla siebie zawsze przecinał brzozę - mimo, iż w innych symulacjach miał też 5mm grubości.
CFD JORGENSENA - czy on cokolwiek z tego rozumie?
Jorgensen przedstawił interpretację fragmentu wykresu kąta przechylenia z raportu KBWL.
Rys.3
Nie ma ona pokrycia w zarejestrowanym wychyleniu prawej lotki, które rosło już przed tym fragmentem (Rys.3). Na wykresie wychylenie spoilera jest proporcjonalne do wychylenia lotki, więc nie ma potrzeby go tu pokazywać. Poza tym jego koncepcja zdradza, że nie ma pojęcia, tworzeia jakiej skali momentów wymaga od lotki.(refareat M.J. na I KS)
Pokazanie przez Jorgensena rozkładu czegoś tam wzdłuż półrozpiętości skrzydeł w zamierzeniu miało znokautować opracowanie Grzegorza Kowaleczki posługującego się między innymi rozkladami otrzymanymi poprzez obliczenia przy pomocy aparatu mechaniki środowisk ciągłych.

Rys.4
Pierwsza wątpliwość, jaka się rodzi, to dlaczego w poblizu kadłuba (żółte prostokąty ) wykresy dla prawego i lewego skrzydła różnią się. Te części są oddzielone gongolami podwozia są od pozostałej części skrzydła, na której jest spoiler i lotka i to, co dzieje się na zewnątrz podwozia, nie powinno mieć wpływu na rozkłady pomiędzy podwoziem i osią kadłuba..
Przyjrzyjmy się dokładnie końcowym fragmentom wykresów które zacieniowałem na różowo, kóre odpowiadają urwanemu fragmentowi skrzydła.
Wykresy dla 10 i 15 stopni, które na poprzednim fragmencie wizualnie zachowują proporcjonalność do kąta natarcia, nagle stają się trudno rozróżnialane, podczas gdy wykres dla 5 stopni leży niżej.
Wszystkie trzy wykresy z wychyloną lotką (skrzydło prawe) falują, podczas gdy z lotką niewychyloną tylko ten dla 10 st.
Ten fragment wykresu jest najprawdopodobniej bezmyślnie improwizowany. Jedynie wykresy dla 10 stopni z wychyloną i niewychyloną lotką na pierwszy rzut oka wyglądają spójnie.
O ile można się domyslić, że ośi x to odległość od osi kadłuba w metrach, to znaczenie skali y jest nieznane.
Wykresy sprawiają wrażenie wykonanych dosyć nieudolną ręką i to w niedoczasie. Przy użyciu stosunkowo prostych metod i darmowych programów skan z książki można doprowadzić do postaci znacznie lepiej udającej profesjonalny produkt, zaś uzyskanie czegoś pokazanego przez Jorgensena przy pomocy komercyjnego narzędzia jest wykluczone.
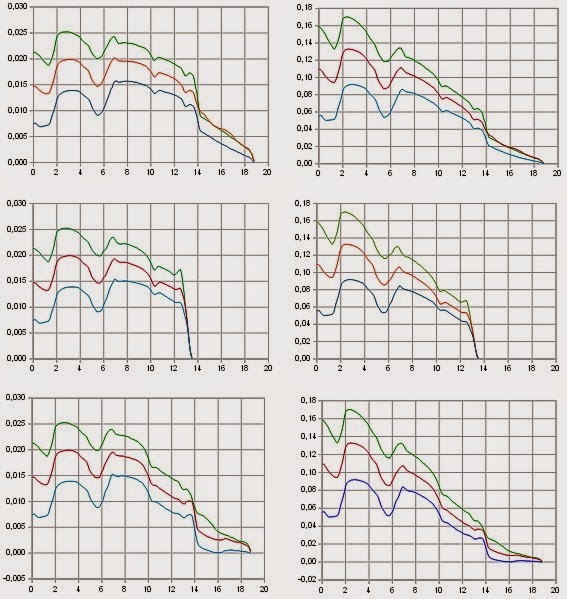
Lewą część rozkładu odbiłem, aby lepiej korespondowała z następnymi wykresami. Następnie zdgitalizowane wartości "zortorektyfikowałem" (trzeba być trendy) przy pomocy dolnej osi i napisów oraz wstępnie znormalizowałem tak, żeby dla każdej trójki wykresów odpowiadających jednemu kątowi natarcia dystrybyanty rozkładu od osi do drugiego minimum (gondola podwozia) były sobie równe. Fizyczny sens tego jest taki, że jest to część skrzydła separowana gondolą, samym podwoziem oraz grzebieniami aerodynamicznymi od tej, gdzie jest spoiler i lotka na prawym skrzydle, a lewe zostało pozbawione końca i w tym obszarze siły nośne powinny być równe na obu skrzydłach. Na wykresach (Rys.5, 6, 8 i 9 ) kolor czerwony to rozklad dla lewego skrzydła, a niebieski dla prawego z wychyloną lotką - na wykresie Jorgensena przerywane linie. Rozkład współczynnika siły nośnej wyrażam w pikselach - tak jak się zdigitalizowało, ponieważ trudno powiedzieć, co Jorgensen miał na myśli, oznaczając na osi zmiennej zależnaej trudne do odczytania liczby, których znaczenia nie udało się ustalić u najbardzziej do krynicy prawdy zbliżonego blogera. Dla dalszych rozważań istotne jest założenie, że wszystkie rozkłady wyrażone sa w tych samych, znanaych, badź nie, Jorgensenowi jednostkach oraz, że zwężenie skrzydła wynosi 3,484 - relacje liczb i wnioski pozostaną takie same. W dalszych rachunkach rozkłady skaluję, mnożąc przez taki czynik, aby po scałkowaniu z lokalną długością cięciwy siła nośna wynikająca z rozkładu dla 5 st. odpowiadała 1g.
Przyglądnijmy się jednemu z tych rozkładów.
Rys.5
Z rozkładu współczynnika wyliczam rozkład siły nośnej. W prawym górnym rogu wykresu wypisałem całkowite siły dla skrzydła i tworzone przez nie momenty obrotowe.
Rys.6
Dla kąta natarcia 5 stopni momenty tworzone przez lewe uszkodzone i prawe z wychyloną lotką oraz spoilerem skrzydla są niemal równe. Dla większych kątów natarcia prawy moment będzie większy od lewego - wychylenie w górę lotki i spoilera nie jest w stanie wystarczająco zmniejszyć siły nośnej. Jest to, zgodne z dobrze znanym wykresem z opracowania NASA i wydaje się, że pod ten nagłośniony wykres było tworzone. Z opracowania NASA wynika, że utrata fragmentu skrzydła o półrozpietosci 26 do 33 % jest możliwa .do skompenowania wychyleniem przeciwnej lotki, jeżeli samolot leci z kątem natarcia 3,5 do 5 stopni. Utrata fragmentu skrzydła to tak jakby wytworzenie na stałe na tym fragmencie zerowego współczynnika siły nośnej. Żeby to skpompensować, trzeba na jego odpowiedniku po przeciwnej stronie wytworzyć zerową wypadkową siłe nośną ( precyzyjnej - zerowy moment siły nośnej). Uwaga - lotka nie jest na całym fragmencie - na zmianę kata natarcia na fragmencie bliższym kadłuba nie ma wplywu - tam kąt natarcia pozostaje taki, jaki był i współczynnik siły nośnej (poza zaburzeniami na granicy) też. Wobec tego na obszarze z lotką trzeba wytworzyć ujemną siłę nośną, ujemny kąt natarcia, ujemny współczynnik siły nośnej. Jorgensenowi, kiedy dorysowywał ten fragment, zabrakło wyobraźni - jeżeli jest to przypadek kąta natarcia, przy którym urtatę fragmentu skrzydła można zrekompensować wychyleniem przeciwnej lotki, to na Rys. 5 w miejscu lotki ujemny.

Rys.7
Wyjaśnienie przyczyny ograniczeń kąta natarcia oraz oszacowanie kąta, dla jakiego, bliską smoleńskiej utratę fragmentu skrzydła, można zrównowazyć wychyleniem przeciwnej lotki, zawarłem w (
http://mjaworski50.blogspot.com/2014/07/beczka.html . Tam też jest bardzo proste geometryczne wyjaśnienie, że lotka wychylając się o 20 stopni może zmienić lokalny kąt natarcia o okolo 6 stopni, więc przy mniejztch kątach natarcia lokalny współczynnik siły nośnej na fragmencie z lotką będzie ujemny.
Przejdźmy do rozkładu dla 10 stopni kąta natarcia, którego wzrokowa ocena wygląda pozytywniej.

.
Rys.8
Tak wygladają wyliczone z niego rozkłady siły nośnej.
Rys.9
Rozkład uzupełniłem o pośredni, ponieważ, bez względu na to, czy rozkłady Jorgensena są prawidłowe, prawa lotka w ostatnich sekundach nie przez cały czas jest maksymalnie wychylona, ale średnio o -11 stopni przy położeniu neutralnym -1 st. (Rys.10) i do rachunków należało by raczej brać kombinację rozkładu szarego i niebieskiego w proporcjach 0,46 do 0,56
.

Rys.10
Z obu rozkładów wynika ekscentryczne pojmowanie przez Jorgensena geometrii utraty fragmentu skrzydła.
Dla kąta natarcia 5 st. promień dla momentu utraconej siły nośnej wynosi:
(2676kNm - 2092kNm)/(383kN - 339kN) - 13,1m a dla kąta natarcia 10 st.:
(3602kNm - 2699kNm)/(537kN - 468kN) - 13,2m .
Wynika z tego, że Jorgensenowi w obu przypadkach odleciały nie całe fragmenty -
na skrzydle pozostały punkty przyłożenia siły nośnej! (taka sytuacja jest możliwa dla obiektów o topologicznych własnościach rogalika, ale urwany fragment ma własności kromki - jest wypukły).
Jak można się było po wyglądzie końcówek spodziewać, analiza iloścowa końcówek wykresów wypada dla autora druzgocąco.
Rys.11
Dla lepszej przejrzystości pokazuję końcówki tylko dwóch wykresów siły nośnej
(linia przerywana to - jak u Jorgensena rozkład siły nośnej po maksymalnym wychyleniu lotki i spoilera ). W tabelce zawarłem wartosci siły nośnej przypadające na fragment skrzydła ze spoilerem
(niebieski na Rys. 5), fragment z lotką
(czerwony na Rys. 5) oraz odstęp pomiędzy nimi. Nie wypisywałem danych dla wychylenia lotki, tylko związany z tym spadek siły nośnej na danym fragmencie.
Rys. 12
Rys. 12a
Jedynie wartości dla fragmentu ze spoilerem pozostają ze sobą w sensownym związku i zostały najprawdopodobniej jakoś przekształcone z prawidłowego rozkładu. Pozostałe są chaotyczne, a są to dane dotyczące fragmentu, który miał się urwać. Siła nośna dla 10 i 15 stopni wytwarzana przez ten fragment przy 10 i 15 stopniach kąta natarcia jest taka sama. Rys.12a przedstawia zmianę siły nośnej wywołaną wychyleniem spoilera i lotki. Wykresy wszystkich różnice powinny być zbliżone do siebie a róznica rozkładów dla 15st. kąta natarcia wyraźnie odbiega od pozostałych na odcinku mniej więcej pokrywającym się z urwanym fragmentem.
Wniosek może być tylko jeden - ten fragment wykresów został zaimprowizowany, a na spójną z poprzednimi improwizację rozkładu dla 15st. Jorgensenowi zabrakło czasu.
Gdyby Jorgensen, adaptując dla swoich potrzeb gdzieś wynalezione jakieś rozkłady wspólczynnkia siły nośnej policzone CFD, rozumiał fizyczne aspekty zagadnienia, zadbałby, aby nie popaść w absurdy. Niestety, nie dość, że nie rozumie tego, co robi, to jeszcze pokazał lekceważenie słuchacza popełniając niedoróbki graficzne, które wskazałem na początku omawiania "CFD".
Podsumowując ten fragment - wygląd wykresów przedstwiających współczynniki siły nośnej, brak, lub błędna ( to wynika z komentarzy Forda Prefecta, któremu coś udało się odcyfrować ) skali na osi y, oraz wynikające z nich absurdy fizyczne świadczą, iż nie są wynikiem obliczeń CFD ani nawet przyzwoitej adaptacji literaturowego rozkładu. W szczególności wykresy odpowiadające urwanemu fragmentowi są prymitywnie domazane. Używanie ich do jakichkolwiek dalszych wyliczeń nie ma sensu.
Jorgensen z pewnością powtórzył wyniki pochodzące z dawniejszych opracowań. Skoro nie przedstwił nowego, poprawnego pojmowania kątów natarcia, pochylenia i wznoszenia, zostały one uzyskane obliczeniemi przy pomocy błędnego algorytmu. Poniżej skrócona historia bezskutecznego zmagania się Jorgensena ze zrozumieniem, że samolot lata dzięki tajemniczenu kątowi natarcia.
Rys.13
Skoro Jorgensenowi bardzo zależy na uwzglednieniu zmienności kąta natarcia, którego w jego bardzo uproszczonym modelu po prostu nie ma, spróbuję mu pomóc obejśc jego problem. Jak sam napisał, choć nie wiadomo, czy rozumiał, co pisze, siła nośna jest proporcjonalna do kąta natarcia. Tak więc aktualna siła nośna jest proporcjonalna do efektywnego kąta natarcia. Z drugiej strony ta siła nośna jest proporcjonalna do przeciązenia pionowego, a ono jest rejestrowane.
Rys.14.
Siły w kółku nie ma, bo nie ma tego fragmentu skrzydła ( gdyby była, samolot zaczął by się obracać w przeciwną stronę ).
Oznaczmy sobie przez x ułamek utraconej siły nośnej, przez F całą siłę nośną, przez Va rejestrowane przeciążeniae pionowe, przez m masę
( przyjmę 78 200 kg) . Z moich wcześniejszych wyliczeń (
http://mjaworski50.blogspot.com/2014/07/beczka.html ) wynika, że średni promień dla momentu siły uraconego fragmnetu R = 15,5m.
Wtedy
F*(1-x) = Va * m
Zaś równanie obrotu przyjmie postać
I * d(omega)/dt = m*R*Va*x/(1-x)
Przy takim podejściu nie mamy w postaci jawnej składnika tłumienia obrotu.
Moment bezwładności wokół osi kadłuba przyjmuję I = 1670kgm
Całkując dwukrotnie to równanie obrotu i dopasowując kąt przechylenia do zarejestrowanego wyznaczam x W szczegółach procedura przedstawia się nastepująco:
1. Korzystam z modeli przeciążeń pionowych wykorzystując raporty MAK (żólte trojkąty) i KBWL (zielone trokaty). Jako jeden model biorę (3* mniejsze + więkze)/4, jako drugi (3*większe + mniejsze)/4. Powinno to zadośćuczynić niepewności co do rzeczywistych wartości wynikającej z różnic w zarejestrowanych przebiegach.
Rys.15
2. Całkownia wykonuję metodą punktu środkowego.
3. Rozwiązanie dopasowuję do obu zarejestrowanych przebiegów kąta przechylenia minimalizując średniokwadartowe odchylenie względne. Pozwala to wyznaczyć korytarz błędu dla przebiegu ekstrapolowanego na zakres, gdzie pomiary nie wystepują.
a) jako pierwszy przebieg prędkosci przechylenia.
Rys.16
Widać, że po około sekundzie przekracza zakres maksymalny zakres 18 st./s rejestrowany przez MRSP..
b) rozwiązania przy dobranych x dla obu modeli niemal pokrywają się.
Rys.17
Możliwy jest szeroki zakres końcowego przechylenia - obejmujący wartość MAK, KBWL oraz wyliczoną przez Grzegorza Kowaleczkę.
Wartości x to 0,049 dla modelu "mniejszego przeciążenia" oraz 0,0425 dla "większego" czyli około 4,5 %.
c) na koniec wykres siły oraz pogladowy
( uśredniony na odcinek 0,75s ). powodującej obrót.
Rys.18.
Okazuje się, że dla wykonania obrotu powyżej 90 stopni wcale nie jest potrzebna tak duża nierównowaga sił, o jakiej zwykle się mówi. Wystarczy, żeby działała cały czas - wtedy predkość kątowa stale rośnie zamaist osiągnąć wartość asymptoytyczną, czy też maleć, co skutkiem zastosowania błędnego wzoru wyszło Jorgensenowi.
Na podstawie powyższych obliczeń można twierdzić, iż przebiegi przeciążeń, kątów przechyleń oraz podawane w częsciach opisowych raportów wartości kąta przechylenia nie są sprzeczne. Jednakże, biorąc pod uwagę różnice pomiędzy trajektorimi 06.04 oraz 10.04 omawianymi przeze mnie na I KS oraz Marka Czachora 05.02.2013 oraz różnice w prędkościach kątowych generowanych przez lotki uważam, że rejestrowane parametry lotu nie odzwierciedlają się na tyle dokładnie w prędościach i współrzędnych samolotu, iżby można było kusić się o ich dokładne wyliczenie.
JABCZYŃSKI - dowód "z pantofla"
Komentarz ilustracyjny do wystąpienia wschodzącej gwiazdy obywaltelskiego śledztwa smoleńskiego.
.
PRAWDA na razie uciekła
ale będzie goniona przez kolejny rok, a może i dłużej, bo zamykający Konferencję Przewodniczący Komitetu Naukowego przez moment wydawał się watpić w sens organizowania konferencji za rok.